Предпросмотр файла:

Урок – сказка УРОК ГЕОМЕТРИИ В 8 КЛАССЕ
Подготовил:
Учитель математики
МОУ СШ №9 г. Снежное
Козченко Ирина Алексеевна

Тема: Решение задач и упражнений Цель: Обобщать и систематизировать теоретические знания учащихся о многоугольниках: параллелограмме, прямоугольнике, ромбе и квадрате. Сформировать навыки и умения использования свойств многоугольников при решении задач на вычисление, доказательство и построение. Развивать логическое мышление. Воспитывать трудолюбие, умение оценивать свои знания. Задачи: Повторить основной теоретический материал о параллелограмме, прямоугольнике, ромбе и квадрате. Усовершенствовать умения и навыки решения задач по теме «Четырехугольники». Анализировать, делать логические выводы. Научиться оценивать свои знания.

Страна «Многоугольники»

ЧЕТЫРЕХУГОЛЬНИК
Четырёхугольник — это геометрическая фигура ( многоугольник ), состоящая из четырёх точек (вершин), три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.

1.Кто я?
2.Почему вы так решили?
3.Найдете ли вы меня на этих рисунках, объяснив свой выбор?

Параллелограмм
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства: 1 .В параллелограмме противоположные стороны равны и противоположные углы равны 2 .Диагонали параллелограмма точкой пересечения делятся пополам 3 .Углы, прилежащие к любой стороне, в сумме равны 4 .Диагонали параллелограмма делят его на два равных треугольника. 5. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон

- Кто я такой?
- Чем я отличаюсь от остальных жителей страны?
- Найдите меня среди них.

Найдите неизвестные углы, используя таблицы с рисунками.
ПРЯМОУГОЛЬНИК
Прямоугольник — четырехугольник , у которого все углы прямые (равны 90 градусам).
Свойства:
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны
2. Противоположные стороны прямоугольника параллельны
3. Прилегающие стороны прямоугольника всегда перпендикулярны
4. Все четыре угла прямоугольника прямые
5. Сумма углов прямоугольника равна 360 градусов
6. Диагонали прямоугольника имеют одинаковой длины:
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).

Решите задачи, используя таблицы с рисунками.
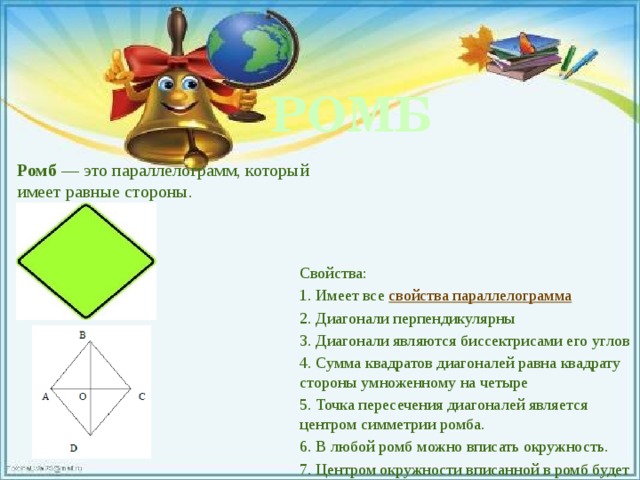
РОМБ
Ромб — это параллелограмм, который имеет равные стороны.
Свойства:
1. Имеет все свойства параллелограмма
2. Диагонали перпендикулярны
3. Диагонали являются биссектрисами его углов
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре
5. Точка пересечения диагоналей является центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
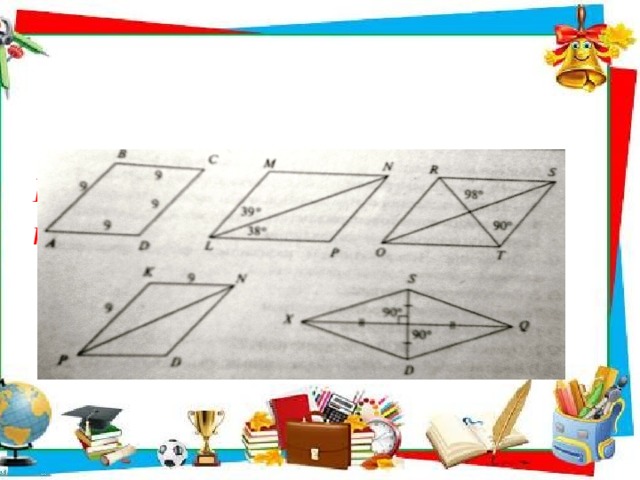
Решите задачи, используя таблицы с рисунками.

КВАДРАТ
Квадрат — это четырехугольник у которого все четыре стороны и углы одинаковы. Квадраты отличаются между собой только длиной стороны, но все четыре угла у них прямые, то есть по 90°.
Свойства:
1. Имеет все свойства параллелограмма
2. Диагонали перпендикулярны:
3. Диагонали являются биссектрисами его углов
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре
5. Точка пересечения диагоналей называется центром симметрии квадрата.
6. В любой квадрат можно вписать окружность.
7. Центром окружности вписанной в квадрат будет точка пересечения его диагоналей.

Вы все очень хороши, все полезны и важны.

ТЕОРЕТИЧЕСКИЙ ТЕСТ ПО ГЕОМЕТРИИ
8 КЛАСС
ТЕМА: ЧЕТЫРЕХУГОЛЬНИКИ
А1. Сумма углов выпуклого n-угольника равна:
1) 180°(n − 2)
2) 360°
3) 180° · n
4) 360° · n
А2. Четырехугольник является параллелограммом, если у него:
1) две стороны равны, а две другие параллельны
2) диагонали пересекаются и точкой пересечения делятся пополам
3) две пары равных сторон
4) все стороны параллельны
А3. Прямоугольником называется:
1) параллелограмм, у которого все стороны равны
2) параллелограмм, у которого все углы прямые
3) четырехугольник, у которого диагонали равны
4) четырехугольник, у которого противолежащие стороны равны

А4. Четырехугольник является ромбом, если у него:
1) диагонали перпендикулярны
2) диагонали равны
3) диагонали перпендикулярны и точкой пересечения делятся пополам
4) диагонали точкой пересечения делятся пополам
А5. Квадратом является:
1) параллелограмм, у которого все углы прямые
2) ромб, у которого все углы прямые
3) параллелограмм, у которого диагонали равны
4) прямоугольник, у которого диагонали равны
А6. Всякий прямоугольник является:
1) квадратом
2) ромбом
3) трапецией
4) параллелограммом

А7. Выберите верное утверждение:
1) если в четырехугольнике диагонали равны и точкой пересечения делятся пополам, то этот четырехугольник — прямоугольник
2) если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник — ромб
3) если в четырехугольнике две стороны равны, а два угла прямые, то этот четырехугольник — прямоугольник
4) если в четырехугольнике диагонали равны, а один из углов прямой, то этот четырехугольник — квадрат
А8. Внешний угол правильного n-угольника равен:
1) 180° / n
2) 180° (n − 2)/n
3) 360° (n − 2)/n
4) 360° / n
А9. Многоугольник называется выпуклым, если:
1) все его стороны являются выпуклыми
2) его нельзя разрезать на два других многоугольника
3) он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины
4) все его углы являются выпуклыми

СПАСИБО ЗА ВНИМАНИЕ!!!