Предпросмотр файла:
«Геометрия владеет
двумя сокровищами:
одно из них – это
теорема Пифагора»
Иоганн Кеплер


Историческая справка
Пифагор – древнегреческий ученый, живший в VI веке до нашей эры.
Вообще надо заметить, что о жизни и деятельности Пифагора, который умер две с половиной тысячи лет тому назад, нет достоверных сведений. Биографию учёного и его труды приходится реконструировать по произведениям других античных авторов, а они часто противоречат друг другу.

С именем Пифагора связано много важных научных открытий: в географии и астрономии – представление о том, что Земля – шар и что существуют другие, похожие на неё миры; в музыке – зависимость между длиной струны арфы и звуком, который она издаёт; в геометрии – построение правильных многоугольников (один из них пятиконечная звезда – стал символом пифагорейцев).
Венчала геометрию теорема Пифагора , которой посвящён сегодняшний урок.
Но изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно задолго до Пифагора. Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы.
Опорное повторение по готовым чертежам
В
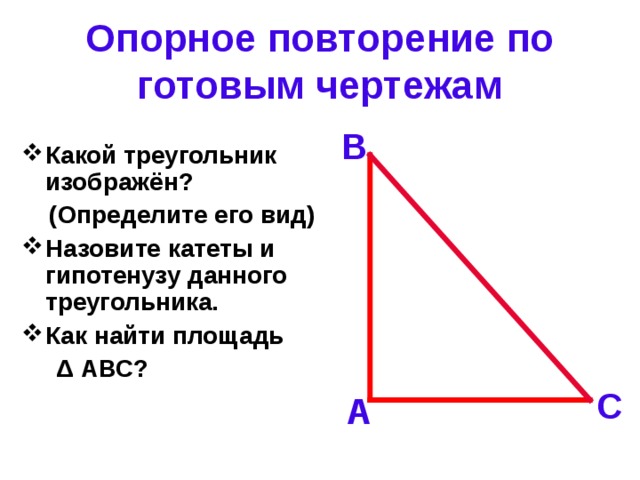
- Какой треугольник изображён?
(Определите его вид)
- Назовите катеты и гипотенузу данного треугольника.
- Как найти площадь
Δ АВС?
С
А
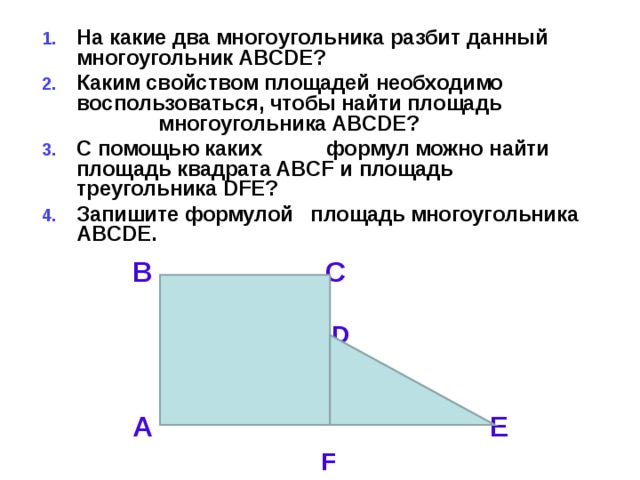
- На какие два многоугольника разбит данный многоугольник ABCDE?
- Каким свойством площадей необходимо воспользоваться, чтобы найти площадь многоугольника ABCDE?
- С помощью каких формул можно найти площадь квадрата ABCF и площадь треугольника DFE?
- Запишите формулой площадь многоугольника ABCDE.
В С
D
A E
F

Практическая работа
- Постройте в тетрадях прямоугольный треугольник (с катетами, длина которых для удобства выражается целыми числами). Измерьте катеты и гипотенузу. Результаты измерений запишите в тетрадях. Возведите все результаты в квадрат, т. е. Узнайте величины a 2 ; b 2 ; c 2 . Сложите квадраты катетов (a 2 + b 2 ) и сравните с квадратом гипотенузы. У всех ли получилось, что a 2 + b 2 = с 2 ?
- Постройте в тетрадях прямоугольный треугольник (с катетами, длина которых для удобства выражается целыми числами).
- Измерьте катеты и гипотенузу. Результаты измерений запишите в тетрадях.
- Возведите все результаты в квадрат, т. е. Узнайте величины a 2 ; b 2 ; c 2 .
- Сложите квадраты катетов (a 2 + b 2 ) и сравните с квадратом гипотенузы.
- У всех ли получилось, что a 2 + b 2 = с 2 ?
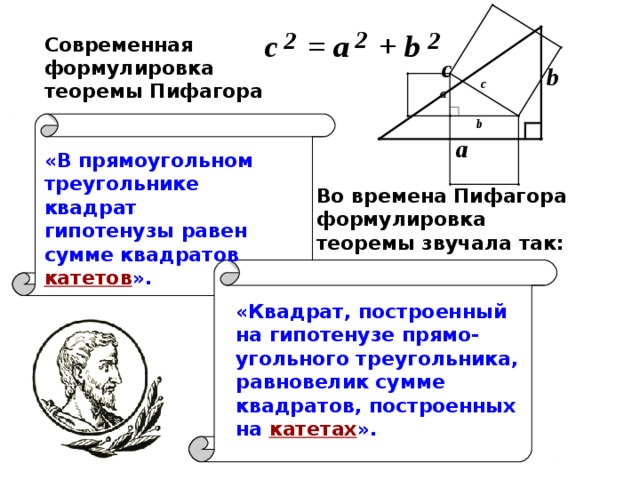
Современная формулировка
теоремы Пифагора
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов катетов ».
Во времена Пифагора формулировка теоремы звучала так:
«Квадрат, построенный на гипотенузе прямо-угольного треугольника, равновелик сумме квадратов, построенных на катетах ».
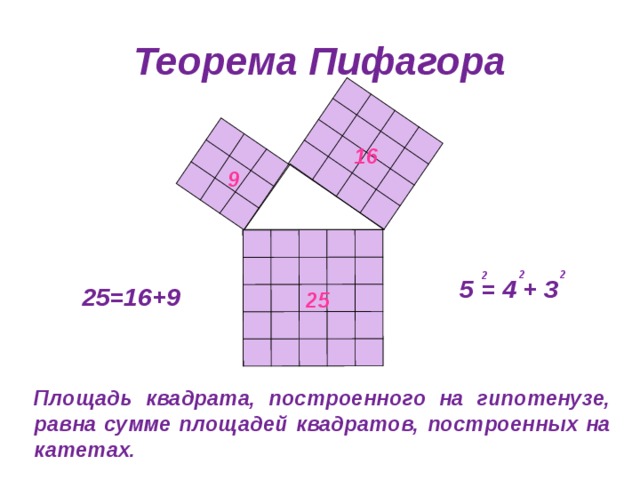
Теорема Пифагора
16
9
2
2
2
5 = 4 + 3
25=16+9
25
Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
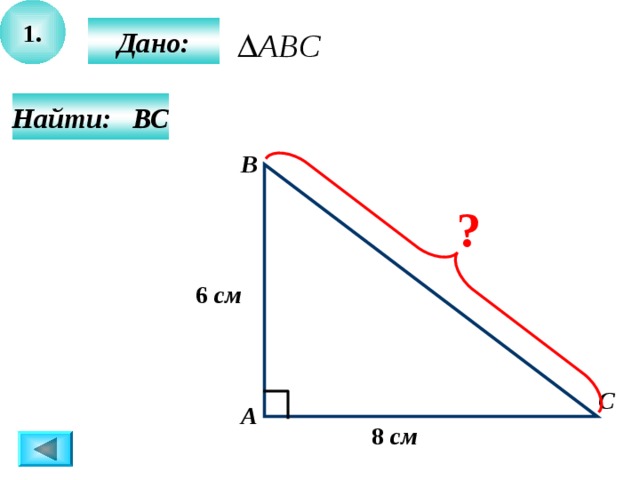
1.
Дано:
Найти: ВС
В
?
6 см
С
А
8 см
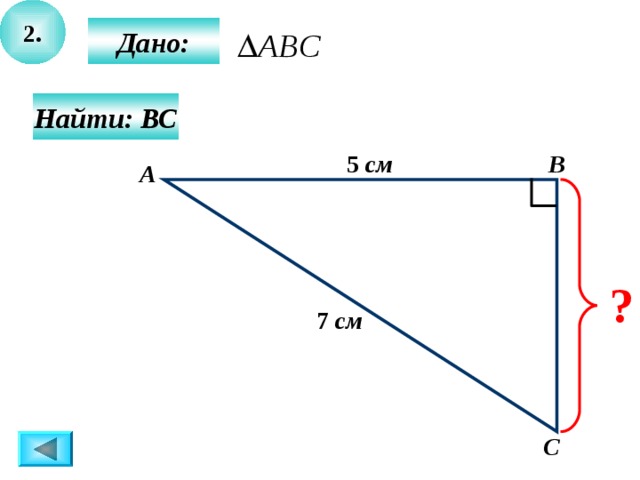
2.
Дано:
Найти: ВС
В
5 см
А
?
7 см
С
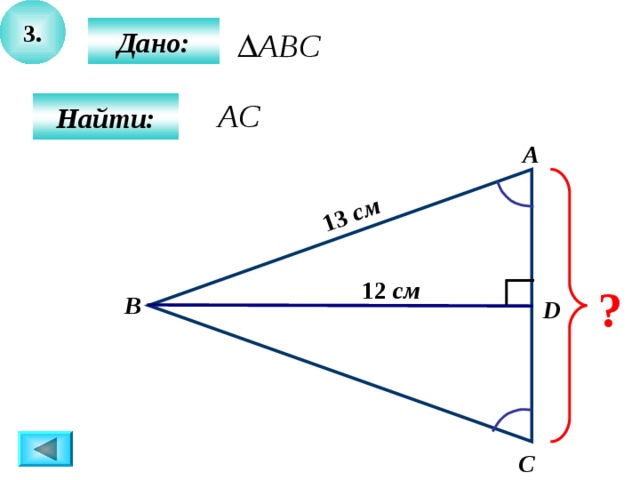
3.
13 см
Дано:
Найти:
А
12 см
?
B
D
C

Пифагоровы штаны
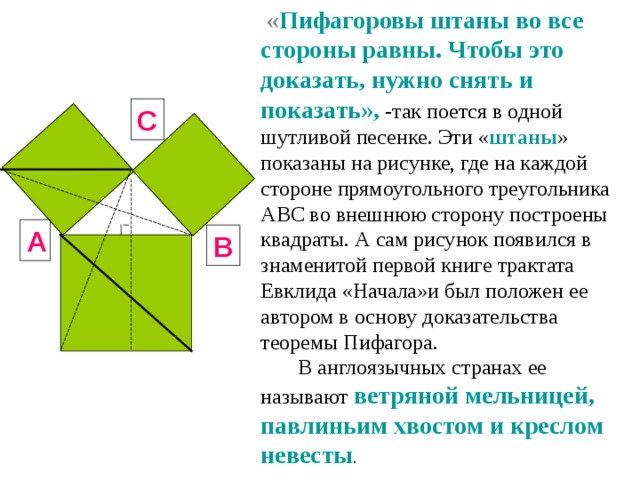
« Пифагоровы штаны во все стороны равны. Чтобы это доказать, нужно снять и показать», -так поется в одной шутливой песенке. Эти « штаны » показаны на рисунке, где на каждой стороне прямоугольного треугольника АВС во внешнюю сторону построены квадраты. А сам рисунок появился в знаменитой первой книге трактата Евклида «Начала»и был положен ее автором в основу доказательства теоремы Пифагора.
В англоязычных странах ее называют ветряной мельницей, павлиньим хвостом и креслом невесты .
C
A
B

Шаржи к теореме Пифагора (из учебников XVI века)

Пифагоровы тройки

Изучение свойств натуральных чисел привело пифагорейцев к ещё одной «вечной» проблеме теоретической арифметики (теории чисел) — проблеме, ростки которой пробивались задолго до Пифагора в Древнем Египте и Древнем Вавилоне, а общее решение не найдено и поныне. Начнем с задачи, которую в современных терминах можно сформулировать так: решить в натуральных числах неопределенное уравнение
а 2 +b 2 =c 2 .

Сегодня эта задача именуется задачей Пифагора, а её решения — тройки натуральных чисел, удовлетворяющих уравнению (а 2 +b 2 =c 2 )— называются пифагоровыми тройками. В силу очевидной связи теоремы Пифагора с задачей Пифагора последней можно дать геометрическую формулировку: найти все прямоугольные треугольники с целочисленными катетами а, b и целочисленной гипотенузой c .
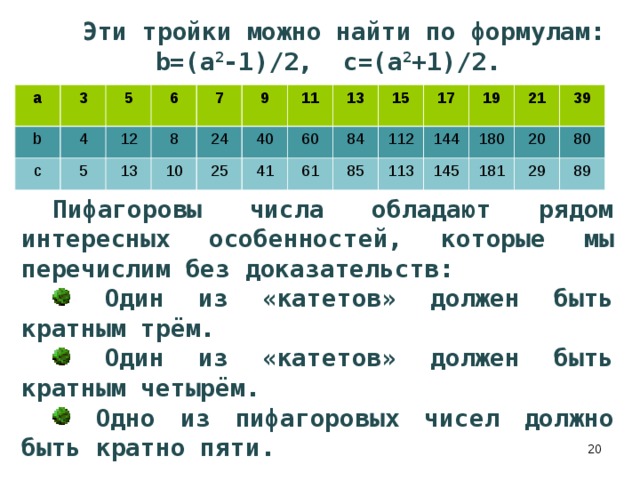
Пифагоровы числа обладают рядом интересных особенностей, которые мы перечислим без доказательств:
- Один из «катетов» должен быть кратным трём.
- Один из «катетов» должен быть кратным четырём.
- Одно из пифагоровых чисел должно быть кратно пяти.
Эти тройки можно найти по формулам: b=(a 2 -1)/2, c=(a 2 +1)/2.
а
b
3
c
5
4
5
12
6
8
13
7
9
24
10
11
25
40
13
60
41
15
84
61
85
112
17
113
144
19
145
180
21
20
39
181
80
29
89
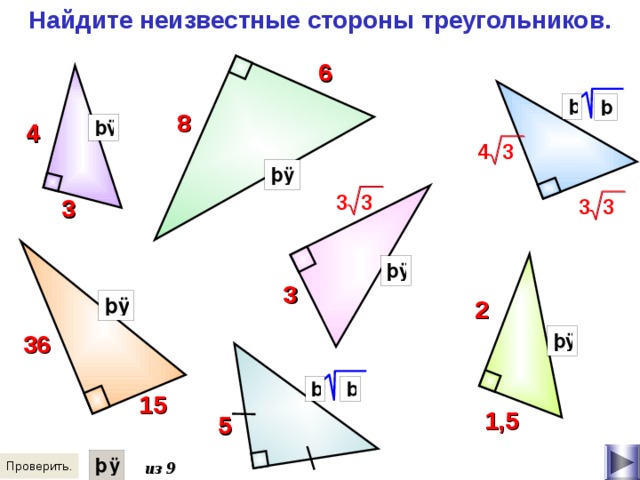
Найдите неизвестные стороны треугольников.
6
8
4
3
4
3
3
3
3
3
3
2
36
15
1,5
5
из 9
21
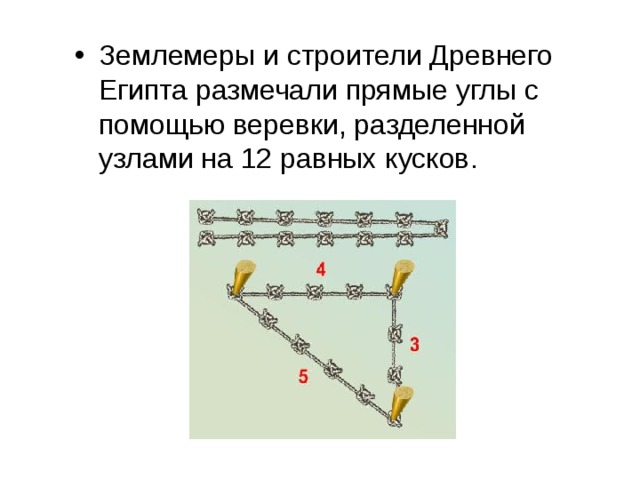
- Землемеры и строители Древнего Египта размечали прямые углы с помощью веревки, разделенной узлами на 12 равных кусков.
Посмотри!
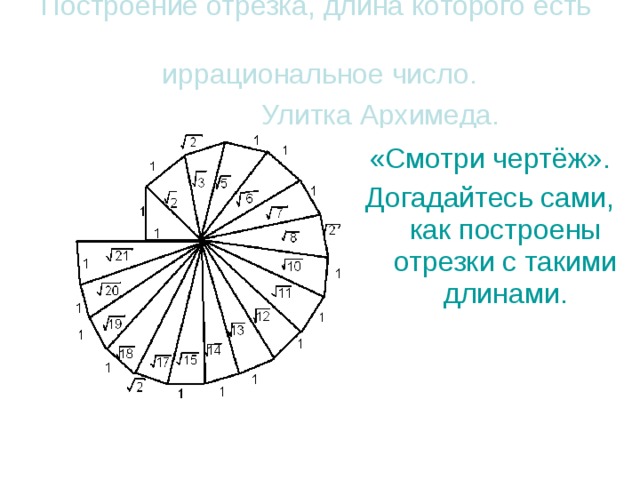
Построение отрезка, длина которого есть иррациональное число. Улитка Архимеда.
«Смотри чертёж».
Догадайтесь сами, как построены отрезки с такими длинами.

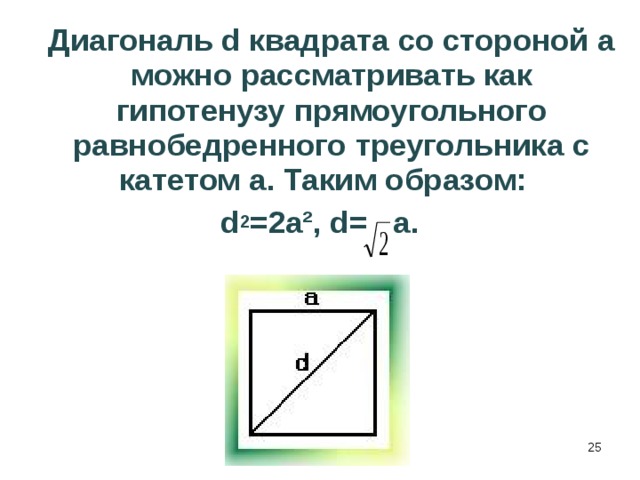
Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом:
d 2 =2a², d= a.
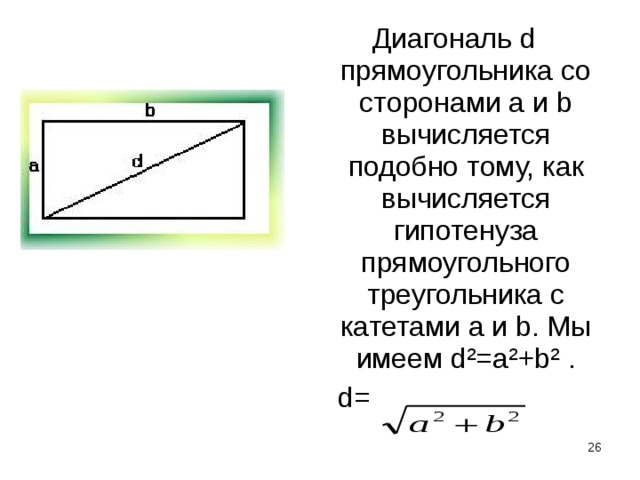
Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем d²=a²+b² .
d=
В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны
1.ширине окна (b) для наружных дуг
2. половине ширины, (b/2) для внутренних дуг
Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра.
В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора.
В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b/2 и r= b/4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4 + p, один катет равен b/4, а другой b/2 — p. По теореме Пифагора имеем:
(b/4 + p) ² = (b/4) ² + (b/2 — p) ²
или b ² /16 + bp/2 + p ² = b ² /16 +b ² /4 — bp + p ² ,
откуда
bp/2 = b ² /4 — bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p = b/4, p = b/6

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы которые долгое время считались исскуственными) и др.
Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора.
Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
НАЗАД


И. Дырченко
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.

О теореме Пифагора
Пребудет вечной истина, как скоро Все познает слабый человек! И ныне теорема Пифагора Верна, как и в его далекий век. Обильно было жертвоприношенье Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За света луч, пришедший с облаков. Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, ее почуя, вслед. Они не в силах свету помешать, А могут лишь закрыв глаза дрожать От страха, что вселил в них Пифагор.
A. Шамиссо

Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“ Как озера вода здесь глубока?”
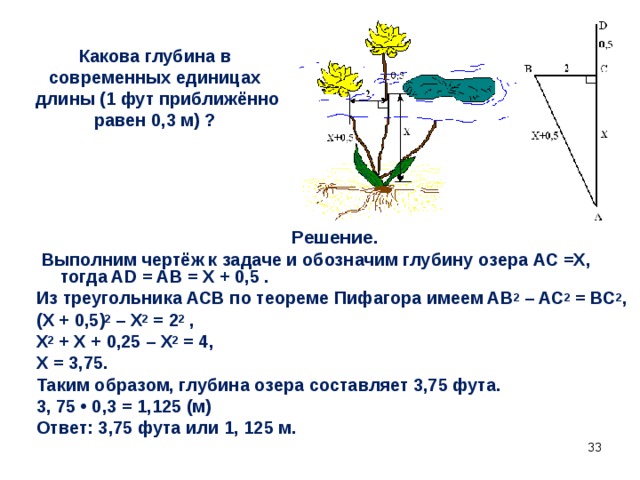
Какова глубина в современных единицах длины (1 фут приближённо равен 0,3 м) ?
Решение.
Выполним чертёж к задаче и обозначим глубину озера АС =Х, тогда AD = AB = Х + 0,5 .
Из треугольника ACB по теореме Пифагора имеем AB 2 – AC 2 = BC 2 ,
(Х + 0,5) 2 – Х 2 = 2 2 ,
Х 2 + Х + 0,25 – Х 2 = 4,
Х = 3,75.
Таким образом, глубина озера составляет 3,75 фута.
3, 75 • 0,3 = 1,125 (м)
Ответ: 3,75 фута или 1, 125 м.

На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки, осталось три фута всего от ствола. Прошу тебя, скоро теперь мне скажи: у тополя как велика высота?

Решение.
Пусть CD – высота ствола.
BD = АВ
По теореме Пифагора имеем АВ = 5 .
CD = CB + BD,
CD = 3 + 5 =8.
Ответ: 8 футов.
Задача Бхаскары

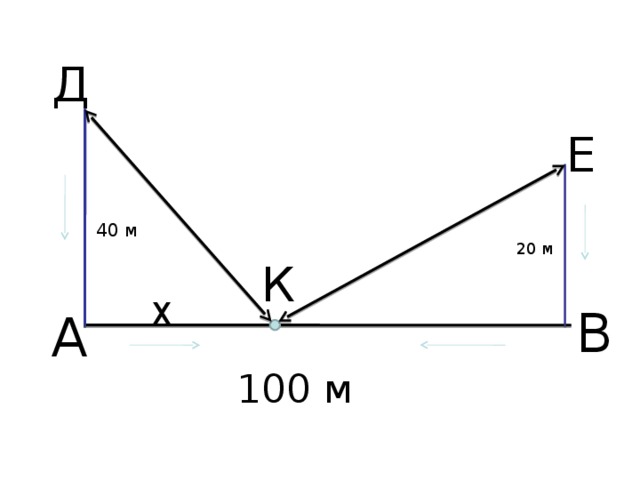
На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?

Решение
Итак, в треугольнике АDВ: АВ 2 =ВD 2 +АD 2
АВ 2 =30 2 +Х 2
АВ 2 =900+Х 2 ;
в треугольнике АЕС: АС 2 = СЕ 2 +АЕ 2
АС 2 =20 2 +(50 – Х) 2
АС 2 =400+2500 – 100Х+Х 2
АС 2 =2900 – 100Х+Х 2 .
Но АВ=АС, так как обе птицы пролетели эти расстояния за одинаковое время.
Поэтому АВ 2 =АС 2 ,
900+Х 2 =2900 – 100Х+Х 2 ,
100Х=2000,
Х=20,
АD=20.
Значит, рыба была на расстоянии 20 локтей от большой пальмы.
Ответ: 20 локтей.
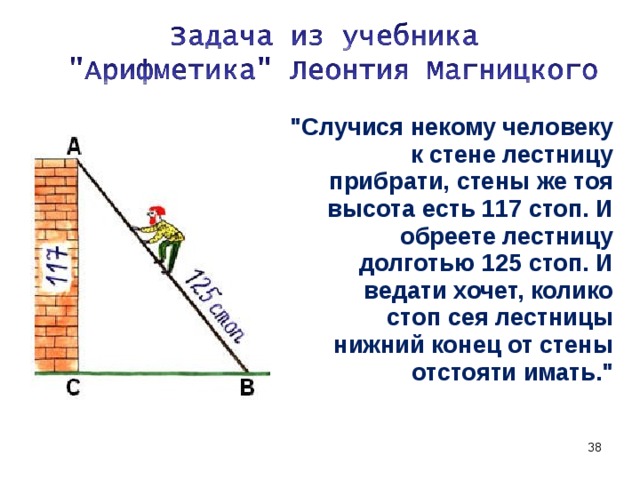
«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.»

«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.
Спрашивается: какова глубина воды и какова длина камыша? «
Д
Е
40 м
20 м
К
Х
В
А
100 м

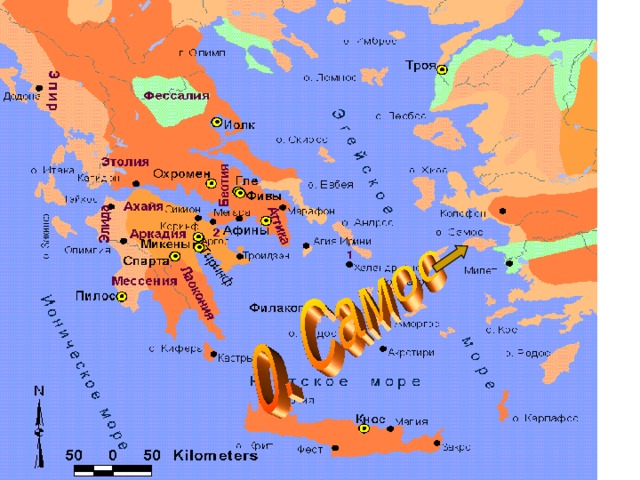
1 Пифагор родился на острове:
а).Родос
б)Крит
в)Мадагаскар
г)Самос
- а).Родос б)Крит в)Мадагаскар г)Самос
3. Выберите верное равенство для данного треугольника:
а)a 2 + c 2 = b 2
б)a 2 + b 2 = c
в)b 2 + c 2 = a 2
г)a 2 + b 2 = c 2
ТЕСТ
Ответ: г
2. Теорема Пифагора гласит:
a)В треугольнике квадрат гипотенузы равен квадрату катетов.
б)В прямоугольном треугольнике гипотенуза равна сумме катетов.
в)В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
г)В прямоугольнике квадрат гипотенузы равен сумме квадратов катетов.
- a)В треугольнике квадрат гипотенузы равен квадрату катетов. б)В прямоугольном треугольнике гипотенуза равна сумме катетов. в)В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. г)В прямоугольнике квадрат гипотенузы равен сумме квадратов катетов.
Ответ: г
4. Выберите тройку пифагоровых чисел:
а)2, 3 и 5
б)4, 5 и 8
в)5, 12 и 13
г)9, 11 и 14
- а)2, 3 и 5 б)4, 5 и 8 в)5, 12 и 13 г)9, 11 и 14
Ответ: в
Ответ: в

Изречения Пифагора
- Статуя формой своей хороша, А человека украсят дела.
- Шуткой беседу укрась, освети. Шутка, что соль. Лишь не пересоли…
- Лучше молчи, ну, а коль говоришь, Пусть будет лучше, чем то, что молчишь.
- Если ты в гневе, не смей говорить! Действовать резко и злобу сорить.
- Пред тем, как станешь говорить, пусть мысль созреет Под языком твоим. Созревшая — все смеет.

Память.
Памятник Пифагору находится в порту города Пифагория и напоминает всем о теореме Пифагора, наиболее известном его открытии. Катет, лежащий в основании треугольника — мраморный , гипотенуза и фигура самого Пифагора в виде второго катета — медные.