Предпросмотр файла:
ТЕМА УРОКА: «Показательная функция, ее свойства и график»
Цели:
-
ввести определение показательной функции;
-
сформулировать её основные свойства;
-
показать построение графиков функции
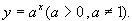
План урока:
-
Проверка домашнего задания
-
Объяснение нового материла
-
Работа у доски
-
Работа в парах
-
Итог.
Ход урока:
1) Проверка Д/З. Учитель вызывает к доске учащихся, которые на доке показывают решение некоторых примеров из Д/З.
-
Объяснение нового материала:
Учитель сообщает тему урока, цели. На проекторе слайд №1, 2,3 (см презентацию)
-
Функцию вида y=ax, где а0, a≠1, х – любое число, называют показательной функцией.
-
Область определения показательной функции: D (y)=R – множество всех действительных чисел.
-
Область значений показательной функции: E (y)=R+ — множество всех положительных чисел.
-
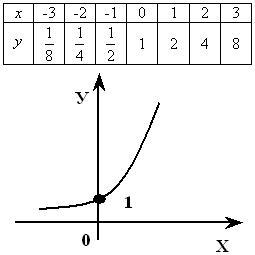
Показательная функция y=ax возрастает при a1.
-
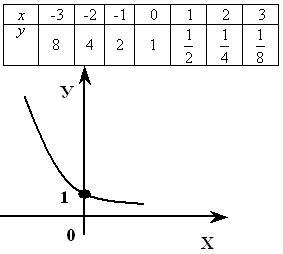
Показательная функция y=ax убывает при 0.
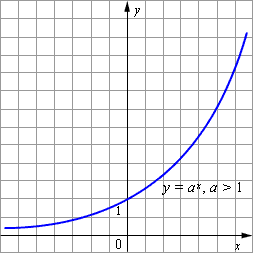
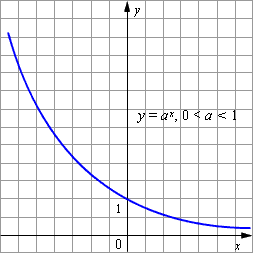
К общим свойствам показательной функции как при 0 a 1 относятся:
Построить графики функций: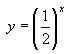 
Построить графики функций: и
.
|
|
|
|
|
|
Задание для выполнения у доски: В одной координатной плоскости построить графики функций:
y=2x, y=3x, y=5x, y=10x. Сделать выводы.
График функции у=2х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.
(Слайд презентации № 6)
Выводы:
1) Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
2) Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание а (если a1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
3) Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Сделать задание в тетради (первые 2 учащихся получают отличные оценки):
y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x. Сделать выводы. . (Слайды презентации № 7)
Смотрите построение графика функции y=(1/2)x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.
1) Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R+.
2) Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
3)Чем меньше основание а (при 0х, тем ближе расположена кривая к оси Оу.
4) Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Решить графически уравнения: (Слайды презентации № 
1)) 3x=4-x. Даная задача решается одним учеником у доски, с помощью учителя
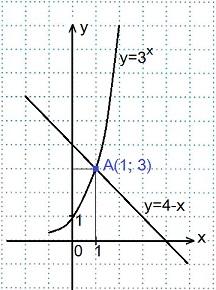
В одной координатной плоскости построим графики функций: у=3х и у=4-х.
Графики пересеклись в точке А(1; 3). Ответ: 1.
2) 0,5х=х+3.
Данное задание учащения решают самостоятельно.
Ответ по истечению 3-5 мин. появляется на доске.
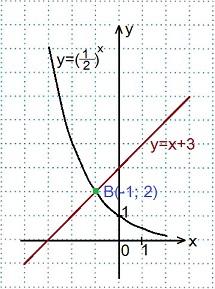
В одной координатной плоскости строим графики функций: у=0,5х (y=(1/2)x )
и у=х+3. Графики пересеклись в точке В(-1; 2). Ответ: -1.
Найти область значений функции: 1) y=-2x; 2) y=(1/3)x+1; 3) y=3x+1-5. .
(Слайды презентации № 9)
Первый пример учитель объясняет подробно на слайде. Остальные учащиеся выполняют самостоятельно.
Решение.
1) y=-2x
Область значений показательной функции y=2x – все положительные числа, т.е.
0x
— ∞x
Ответ: Е(у)=(-∞; 0).
2) y=(1/3)x+1;
01/3)x1, получаем:
0+11/3)x+11;
11/3)x+1
Ответ: Е(у)=(1; +∞).
3) y=3x+1-5.
Запишем функцию в виде: у=3х∙3-5.
0x3:
0∙3x∙33;
0x∙35:
0-5x∙3-5-5;
— 5x∙3-5
Ответ: Е(у)=(-5; +∞).
Итог урока:
Учитель:
Что нового мы узнали на уроке?
Какую функцию называют показательной?
Какие виды показательной функции вы знаете?
Оценивание учащихся. Сообщение домашнего задания: параграф 11 стр 72,
№ 196 (чет) стр 76, № 197 (чет) стр 76
